ResMed Adapt SV vs. Respironics Auto SV

Snooze_Blues wrote:Anybody have an off-the-cuff estimate of what type media (e.g. 8.5 x 11, disc, tractor feed paper, etc.) and the weight and volume of my PSG "graphics"?

Usually one or two pages of the 5 to 7 page complete report, plain ol' paper.

Banned wrote:

StillAnotherGuest wrote:Learn Circuit will pass without the Pprox line.

Holy %#@&*! SAGs right again, duh! When you disconnect the Pprox line and cover the Pprox connector, learn circuit works just fine. So what if rather than tying the Pprox line in a knot, I plugged the Pprox connector with chewing gum and went to sleep? But, before I do that, has anyone done it at the center?

No. Actually, I was just making a calculated guess. I don't want to wreck a $4000 machine.

Here's another one. If Pprox participates in Learn Circuit, then a mask with significant restriction (like nasal pillows) that causes the Learn Circuit to fail, should pass if Pprox is disconnected.

SAG

[quote="Banned"]Nice synopsys, dsm. I'm going to be titrated on 3-day trial with a BiPAP Auto SV at the end of April, even though I use an VPAP Adapt SV. Would it necessarily make a difference which machine I was titrated on?

Banned

[quote="-SWS"]DSM, the ASV manual calls for Learn Circuit to be run when adding more dead space, such as a humidifier.

What do you think of the notion that Learn Circuit may derive: 1) dead-space oriented (fluid) dynamic impedance (which is mathematically flow-directional and thus positive/negative) along with 2) a typical non-dynamic fixed resistance?

The humidifier dead-space purpose of Learn Circuit along with that formula SAG posted (with K1 and K2) strongly corroborate a need to ascertain dynamic impedance (which includes a reciprocal of mask flow conductance).

Just a thought...

SAG wrote: If Pprox participates in Learn Circuit, then a mask with significant restriction (like nasal pillows) that causes the Learn Circuit to fail, should pass if Pprox is disconnected.

Sounds as if Pprox is used to calculate the static resistance portion only (recall your previous Ohm's Law static equation via Pprox). If Pprox completely faults (or does not participate for any reason), then a fall back constant is used for K2 (either recent-session derived or perhaps even taken from a nominal-fit table based on dynamics measurement techniques described below). In that second case Learn Circuit will pass.

Looks as if the (fluid) dynamic portion of the Learn Circuit impedance equation is always derived with the machine-end sensor via highly dynamic time-domain reflection measurements: launch a series of very sharp step or pulse function waves, then measure multiple reflected magnitude data-points toward a "best-fit" determination of a K1 constant to work with (during subsequent in-session K1 & K2 based signal leak differentiation).

Alternately (to above pulse or step functions) other more "motor friendly" wave functions might be used toward measurement of various dynamically reflected magnitudes pursuant determination of those K constants. But this part always needs to be done from the machine and not the proximal end (as a purely dynamic function of time-domain wave reflection).

Pure conjecture on my part, albeit a viable K1 & K2 determination method IMHO. There are always many ways to skin those proverbial cats.

SWS

Just a thought for you but hours of analysis for me

Will get back when I have thought it thru (which could be days even)

DSM

Gentlemen
Interesting discussion, but I too need to really think about it, and especially when I'm not soo tired at the end of the day.

That's what I like about complex posts on this site - it makes you think and work to understand the how and why these more complex machines work and then one can better appreciate how they can help for a given case.

Nice to see you last week in Oz, DSM, on your home turf.

Still working off the jet lag.

Lubman

Lubman,

Ditto

DSM

I'm still working off the beer & wine

D

SWS,

1st reply - you use the words 'dead-space' in relation to a humidifier but I have always understood deadspace in cpap parlance to be space (such as the hollow in a f/f mask) but particularly that part between the nose / mouth and the fixed vent holes.

I.E. shift the vent holes 6 inches up the airtube (or by way of an airtube extension) and the deadspace has grown by that extra space between the mouth/nose & the new location of the vent holes.

I don't see how someone breathing out against the machine say at 8 CMS and with say an Ultra Mirage F/F mask, is going to have any CO2 get any way up the 6ft tube to the humidifier.

So, I am guessing that your use of deadspace is another meaning ?

DSM

PS

Putting a humidifier in the circuit is going to create a damper on the air flow (place where moving air will enter & expand then compress again at the exit & pick up oscillations from ripples on the water plus become slightly heavier as moisture is collected. All that is going to do is make it just that bit harder to get crisp readings on the machines internal flow-sensors & pressure-sensors. If the Prox line input gets too out of whack with the airline sensed input (machine end) then I can understand the LC rejecting the mask.

D

_________________

CPAPopedia Keywords Contained In This Post (Click For Definition): humidifier, mirage, CPAP

-SWS wrote:Sounds as if Pprox is used to calculate the static resistance portion only (recall your previous Ohm's Law static equation via Pprox).

I told you Ohm did more than make light fixtures.

-SWS wrote:If Pprox completely faults (or does not participate for any reason), then a fall back constant is used for K2 (either recent-session derived or perhaps even taken from a nominal-fit table based on dynamics measurement techniques described below). In that second case Learn Circuit will pass.

Not necessarily. Pprox could be involved in a basic measurement of resistance R = P/V (or Ohm's Law where P2 = 0). From a practical point of view, if you stayed with the mask selection, the interface really shouldn't add all that much resistance. Further, since the interface occurs after the Pprox measurement, you're not measuring the effect of it's resistance anyway. You're really just saying, "Well, if the system resistance is >x cmH2O based on R = Pprox - Patm / V, then Learn Circuit fails." Yanking out Pprox simply takes P1 and gives it a value of Patm.

-SWS wrote:Looks as if the (fluid) dynamic portion of the Learn Circuit impedance equation is always derived with the machine-end sensor via highly dynamic time-domain reflection measurements: launch a series of very sharp step or pulse function waves, then measure multiple reflected magnitude data-points toward a "best-fit" determination of a K1 constant to work with (during subsequent in-session K1 & K2 based signal leak differentiation).

Alternately (to above pulse or step functions) other more "motor friendly" wave functions might be used toward measurement of various dynamically reflected magnitudes pursuant determination of those K constants. But this part always needs to be done from the machine and not the proximal end (as a purely dynamic function of time-domain wave reflection).

Pure conjecture on my part, albeit a viable K1 & K2 determination method IMHO. There are always many ways to skin those proverbial cats.

I think we (Whoops! I mean "the discussion group") is drifting away from the significance of the



equation. IMHO, as I see it, in my view (assorted other expressions of disclaim):

It's only used if there is no actual measurement of Pmask;

If you're using it, there are no further calculations performed, everything in there except flow is fixed and unable to account for bacteria filters, humidifiers, etc.;

It's function is only to determine the drop in pressure (measure Pmask without actually measuring Pmask;

It is more accurately represented as the determination of the Sum of Flows (Turbulent + Laminar); and

If Pprox measures Pmask then K1 - K2 is off the table.

SAG

SAG, I have a proposed idea about Snooze's stuff. If you get Snooze's PSG toward your own professional analysis and group discussion, would you mind consolidating that in a separate thread? IMHO that upcoming discussion is going to yield way more benefit to this message board than our present esoteric line of discussion. And my fear is that those far-more-beneficial concepts are going to get lost in this now-arcane thread.

On that note, let's continue trading ideas about this current topic. Naturally, I have differing speculative/interpretive views about some of the stuff in your most recent post. This is a very cool topic for exploration. Once you do get started on the Snooze stuff, we can temporarily pause this esoteric topic and resume it later if you'd like. Hey, I realize you have work and family obligations. On that note I'm still tied up with client work (which is why I have yet to post more of my own take regarding intended use and system impact of these equations).

But I'll at least attempt to address what I think LC's purpose is with respect to learning that circuit impedance (Resmed states LC's primary purpose as being factor-determination of circuit impedance)---and how K constants (capable of being derived in an entire variety of ways) can be used both dynamically, toward transient leak-signal differentiation (proximal sensor thus required----namely toward achieving adequate transient-signal sensitivity), and even toward mean flow through leak calculations (proximal sensor thus not required----as in the much more "mean-value oriented" and thus understandably "transient-signal-dismissive" Malibu case).

This is a very cool topic! But it also feels as if it is a guilty pleasure for but a very few of us (with me being one of the guilty ones). Snooze's stuff, and helping others, really has to take priority---at least in my guilty mind. .

DSM, thanks for that reply! Sounds like we'll probably delve a bit more into some of those fascinating concepts.

Lubman, great to see you!!!

ResMed introduces the (patient data friendly) enhanced VPAP Adapt SV: http://www.vpapadaptsv.com/product.html

Comparison to standard ResMed VPAP Adapt SV parameters:
ASV mode: Min, Max, Default
EEP (cm H2O)* 4, 10, 5
MIN PS (cm H2O)* 3, 6, 3
MAX PS (cm H2O)* 8, 16, 10
CPAP mode:
CPAP (cm H2O) 4, 13, 10
Start CPAP (cm H2O) 4, 13, 4
Ramp (minutes) 0, 45, 20
Max ramp (minutes) 0, 45, 30

* Advanced (Clinician's) menu
(red button and black up/down arrow key, 3 seconds)

The corollary being, of course, that the most complex and automated machine is also the simplest to set-up and operate.

Banned

Reslink and Rescan v3.4 will capture patient friendly data on the new machine. A MS Vista compatible version of Rescan will be released soon.

Banned wrote:ResMed introduces the (patient data friendly) enhanced VPAP Adapt SV: http://www.vpapadaptsv.com/product.html

The AHI measurement capability has to be my favorite of all those upgrades, Banned. What a cool machine!

DSM, I forgot to mention... Yes, thank you for correcting that "dead space" term for me. Indeed, volumetric space is really what I had in mind. I thought I was using the proper biomedical term when, in fact, dead space refers to a biologically-related space in which CO2 is retained after expiration.

SAG wrote:It is more accurately represented as the determination of the Sum of Flows (Turbulent + Laminar).

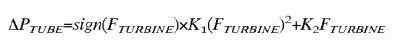
Agreed, SAG. Forgetting, for just a moment, about what gets measured by Learn Circuit, where, and why... I'd like to do some semi-amusing manipulation with that first Ohm's equation you presented. Then I'd like to apply that manipulated Ohm's equation to the above turbulent + laminar flow relationships.

Regarding Ohm's Law SAG Correctly wrote:(Pmachine - Pprox) / Flow = Resistance)

So Ohm's law shows a relationship among: 1) pressure, 2) flow, and 3) resistance. "(Pmachine - Pprox)" can be expressed as "delta P sub tube") as it is in the very first equation presented in this post. From now on, let's just call that "Pdelta" to make typing easier. So I'd like to manipulate the Ohm's law equation by multiplying both sides by "flow" to yield the following Ohm's equation:

Pdelta=(Flow) x (Resistance)
(We'll be using that relationship to manipulate that first equation a bit)

In that first equation, the term "sign(Fturbine)x" translates to either a positive or a minus, depending on the flow direction of the turbine (the word turbine meaning "CPAP impeller"). So let's work the positive or forward-flow case. That makes "sign(Fturbine)x" the same as 1x, which can be dropped as an implied positive sign. That yields the following equation, which we intend to break up into two Ohm's-based equations or components (I'll write Fturbine simply as "Flow"):

Pdelta= (K1 x Flow^2) + (K2 x Flow)

SAG correctly points out that the K1 part of the equation on the left speaks of turbulent flow. He also correctly points out that the K2 part of the equation on the right speaks of laminar flow. Remember that Ohm's Law said that pressure equals flow times resistance. We have some pressure on the left side of that equation and some flow as well as presumable resistance on the right side of the equation. So let's break the above two part equation into two separate Ohm's equations, one for laminar and one for turbulent. Here's the laminar Ohm's expression first since that one's clean and simple so to speak:

Pdelta= (K2 x Flow)
If Ohm's law says that pressure equals resistance times flow, then K2 above must be resistance for the respiratory laminar flow model. Let's do similar Ohm's manipulation with turbulent flow below:

Pdelta= (K1 x Flow^2)
Let's rewrite that as:
Pdelta= K1 x Flow x Flow and then as
Pdelta= (K1 x Flow)Flow

If Ohm's law says that pressure equals resistance times flow, then let's first rewrite the turbulent-case relationship as:
Pdelta= (turbulent resistance) x Flow
(turbulent resistence)=(K1 x Flow) in this fluid-dynamics dirty math trick

A turbulence resistance can be approximately thought of as having a dynamic value as some constant (K1) times Flow. Of course, that's not at all a neat solution in "real" fluid dynamics. Turbulent and laminar flow calculations are nowhere near as simple as the very viable approximations used in respiratory equations. But this rough and extremely dirty math may yield some intuitive insight that a dynamic pressure/flow circuit can be thought of as having some dynamic resistance and some static resistance. The respective resistances are implicitly represented in that K1 and K2 equation that reflects turbulent and laminar flow. Using Ohm's and distributive properties, that very first equation can be viewed with the same "dirty math" to get a feel that (K1 x Flow) more or less represents a dynamic or turbulence-related resistance in that equation while K2 represents a fixed or laminar-related resistance.

Learn Circuit claims to measure circuit impedance to factor in pressure delivery. Regarding "dirty math" toward a paradigm change, you can for all practical purposes think of total circuit impedance in this forward-flow case as being "(K1 x Flow) plus K2". And total circuit impedance in the reverse turbine-flow case can, in similar practicality, be thought of as "negative (K1 x Flow) plus K2". Bearing in mind that fluid dynamics doesn't even come close to being that simple (Poiseuille's and Reynold's aren't even accurate here, but very workable!). The "dirty math" relationship is a very convenient and intuitive approximation regarding a working or practical view of "sum-total dynamic and fixed resistances".

Here's a nice presentation about turbulent and laminar flow in the basic respiratory paradigm or model (for general readership):
http://www.lib.mcg.edu/edu/eshuphysio/p ... ch2_45.htm
Bear in mind the presentation talks about turbulent and laminar flow in the human airway, while this thread has been focusing on similar flow factors inside the machine (with human respiration factored out and turbine rotation factored in).

Entertainment value only, and only intended for those who are not fluid-dynamics purists. If you are a fluid dynamics purist, please let me know so that I can run for cover when I see you or your posse on the streets.

Banned,

In following the link you gave on the Vpap Adapt SV I found this useful link as well

Vpap Adapt SV Titration
http://www.vpapadaptsv.com/documents/10 ... otocol.pdf

And while posting that one we should post this one as well

Bipap AutoSV Titration
http://global.respironics.com/UserGuide ... 042977.pdf


From these you can deduce that the Bipap AutoSV is like a high-powered nascar with manual gear change (manual setting of breathing rate) whereas The Adapt SV is like a formula racing car with a fully automatic gearbox & no manual override.

The Bipap AutoSV because it can set arbitrary breathing rates, can be used to address disordered breathing cases where the rate must be set. The Adapt SV will use the sleepers breathing rate as one of its 90% targets (combined with the MV) so will always vary as the patient varies, within its target.

The Bipap SV is also able to be set up as a CPAP, Bipap, Bipap S/T & SV. That could be a good thing or it could mean a few RTs are going to get quite confused setting it up unless they know what they are setting it up for, then there should be no problem.


DSM

I agree with DSM's characterizations regarding the Resmed ASV as attempting more automation regarding total-parameter "respiratory adjustment". Specifically I'm thinking one huge difference between these two machines is the Resmed ASV's unique objective of adjusting human respiration rate by sliding machine F or "modulation frequency" back and forth. And that alone is a very compelling reason for the algorithm to work with many more respiratory-flow reference points than the Respironics case. Respironics can optionally attempt an automated average-derived backup rate, but that is not quite the same as attempting to continuously and incrementally adjust human respiration rate (by rather fluidly adjusting "modulation frequency").

I think the attempt by Resmed to literally adjust human respiration rate will account for different "will-work"/"won't-work" efficacy patterns when clinically comparing these two machines across large numbers of patients.

Regarding the sports-car analogy: The Resmed sports car attempts to continuously tell the passenger when to breath more quickly or more slowly. The Respironics sports car simply attempts to tell the passenger when he forgot a breath (by initiating that forgotten breath). However, they both attempt to fluidly and adaptively adjust IPAP level or magnitude on an as-needed basis (often "machine-adapting" pressure for each inspiratory breath, toward elimination of suddenly detected central dysregulation).

Thanks for the summary, DSM, and again thanks for that very helpful "dead space" correction!

dsm-
Thank you fort the BiPAP AutoSV titration link. I've always been curious as to how home titration's work. Do they set the machine to factory defaults and then see what pressures were used most during the home study? I'll have to make sure the nurse who gives me the ASV has it set to SV mode, I guess.

-SWS wrote: The Resmed sports car attempts to tell the passenger when to breath more quickly or more slowly while the Respironics machine does not. They both attempt to adaptively adjust the IPAP level on a breath-by-breath basis, as-needed.

SWS-
I may have taken this statement out of context but the ResMed sports car doesn't tell the passenger when to breath more quickly or slowly. In my experience it adapts automatically to my breath flow rate so, as the driver, I tell it when to accelerate or slow down.

What I love about the ResMed VPAP Adapt SV is that it does everything precisely as advertised. There are absolutely no surprises (like the run-away cmH2O) I've heard about. It just quietly chugs along, doing it's thing.

And quiet is an understatement. I cannot hear my machine, only the air filling the mask. I know Casiesea said she could hear crickets, but that machine may have been a pre-production model or gotten some abuse as a demo/titration unit.

As I have learned on this forum, the only application where a patient may do better without an VPAP Adapt SV is shallow-breathing problems, and even that would be suspect if you did as SAG eluded too earlier, spin the dial up until the machine becomes a straight VPAP.

Banned