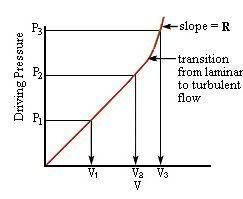
In the original equation of "sum of turbulent plus laminar flows" that squaring turbulent portion was originally derived in that manner to mathematically describe turbulent flow's sum total effect over time toward calculating total flow. Right? That type of end-result or final-equation squaring technique is employed in many steady state equations, especially, to account for very minute "up-and-down" contributions as they are more gradually spread throughout time.SAG wrote:I don't know what that would do. However, for a moment, let's say what SAG said about K1 - K2 is true, that it analyzes activity on a flow wave, and that identifying the integral as "+" or "-" simply defines a segment of the wave. So instead, solving for a point instead of the integral, we're left with Pdelta = K1(Flow)^2 + K2(Flow). The flow in K1 must be squared because in turbulent flow, in order to end up with the same pressure result, the driving pressure needs to be squared. While the K1 - K2 concept considers the phenomena of laminar and turbulent flows in its understanding, it is calculated in terms of resistance, or P/Flow = K1(Flow) + K2.
Contrary to that time-averaging type of calculation, I'm talking about using instantaneous values to decompose circuit-characteristic transitional flow in fluid dynamics, toward table-based circuit identification. What I had in mind was launching turbulent pulse waves in the time domain to:
1) isolate/decompose turbulent and laminar ratio-based component values, based on multiple characteristic discrete point returns
2) specifically use fluid dynamics calculations to arrive at two highly unique sets of discrete decomposed values for turbulent and laminar components (one discrete paired identifier set before pulse launch and another discrete identifier pair after wave-reflection returns, using multiple unique-return pulse or step functions),
3) table-map those multiple discrete paired identifier sets into characteristic function-mapping table entries (not yet the K1 and K2 equation where final squaring occurs)
4) use the returned characteristic table-mapping to return from your "empirically determined" table of circuit-identifying functions, thus returning with K1 and K2 values
5) With those now-identified K1 and K2 values, use flow measurements to plug into the equation below (now squaring that K1 portion), to arrive at pressure loss on the left:
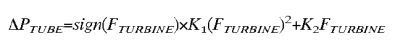
So I wouldn't even propose doing what you have suggested above. What I had in mind is a completely different technique taking advantage of instantaneous values in the time domain (to decompose values for turbulent flow and laminar flow toward table-based circuit identification). And toward instantaneous point-mapping of decomposed values, then an Ohm's-based P/Flow = K1(Flow) + K2 becomes a very practical circuit-identifying equation toward this type of discrete point-based table mapping (the negative turbulence-resistance wisecrack yields a "dirty math trick" chuckle and thus the basis for "running for cover").
Enough said on that proposed algorithmic technique. Resmed may be reflecting waves during Learn Circuit, but I now strongly doubt they're performing a decomposition technique similar to what I have described above. On the notion of wave-reflection even a lowly 0.5 cm FOT is wave-reflection capable. That's why I was wondering about the exact nature of Learn Circuit's pressure output functions.
Regardless, I suspect Resmed may even be able to get by with more basic (unreflected) flow measurements and one-to-one mapping against their "empirically derived" table values for their no-proximal-sensor embodiment.
The proximal-sensor embodiment clearly makes life much easier.
My point is that Resmed's no-proximal-sensor embodiment in the patent description is turbine-flow measured (only) and thus table-derived (that table creation having occurred during Resmed's R&D phase when "empirically determined" entries went into development of that reference table). And if Resmed has that no-proximal-sensor embodiment in their patent description, then they have successfully implemented it. So a compelling question, at least in my mind, is whether that technique still looms in the algorithm for fall-back or at least comparison purposes.
Speaking of looming, ennui of the arcane understandably looms... including here. Me thinks it's time to pack it in. Thanks!